Published : 30 Oct 2019 08:49 AM
Last Updated : 30 Oct 2019 08:49 AM
கதை வழி கணிதம் 4- வித்தியாசமான எண்

இரா. செங்கோதை
ஆசிரியர் வகுப்பறையில் கணிதப் பாடம் எடுத்துக்கொண்டிருந்தார். ஒரு மாணவன், “ஐயா! எங்களுக்கு ஒரு சந்தேகம். நேற்று வகுப்பில் நீங்கள் எந்த எண் 1 மற்றும் அதனாலேயே வகுப்படுமோ அது பகா எண்ணாக இருக்கும் என கூறினீர்கள். அப்படிப் பார்த்தால் 1 என்ற எண் 1 ஆலும், அதனாலும் வகுப்படுமல்லவா? எனவே 1 பகா எண்ணாகத்தானே இருக்க வேண்டும்?” என்று கேள்வி எழுப்பினான்.
“நல்ல கேள்வி, இரண்டாயிரம் ஆண்டுகளுக்கு முன் வாழ்ந்த கிரேக்கக் கணித மேதை யூக்ளிட்‘1-ஐ தவிர்த்து அனைத்து இயல் எண்களையும் பகாஎண்கள் படிகளின் பெருக்கலாக தனித்த வழியில் எழுதலாம்’ என்றார். இதை ‘எண்ணியலின் அடிப்படைத் தேற்றம்’ (Fundamental Theorem of Arithmetic) என இன்று அழைக்கிறோம்” என்று விளக்கம் அளிக்க தொடங்கினார் ஆசிரியர்.
அட ஆமாம்!
எடுத்துக்காட்டாக, 60 என்ற எண்ணை எடுத்துக்கொள்வோம். இந்த எண்ணை 60 = 2 × 30 = 4 × 15 = 3 × 20 = 6 × 10 = 5 × 12 என பலவிதங்களில் பிரித்து எழுதலாம் அல்லவா? என ஆசிரியர் கேட்க, அனைத்து மாணவர்களும் ஒருசேரத் தலையசைத்தார்கள்.
பலவித பெருக்கல்களில் பகா எண்கள் மட்டுமல்லாது பகு எண்களும் இடம்பெற்றிருப்பதைக் கவனித்தீர்களா?
உதாரணமாக, 60 = 2 × 30 என எழுதும்போது 2 என்பது பகா எண்ணாகவும், 30 பகு எண்ணாகவும் இருப்பதைப் பாருங்கள் என ஆசிரியர் மாணவர்களின் கவனத்தை ஈர்த்தார்.
அதேபோல், 60 = 4 × 15 என எழுதும்போது இதில் உள்ள 4, 15 ஆகிய இரண்டு எண்களும் பகு எண்களாக இருப்பதை பாருங்கள். நமது பெருக்கல்களில் பகு எண்கள் இருப்பதாலேயே 60-ஐ பல்வேறு பெருக்கல் வழிகளில் எழுத முடிகிறது.
சபாஷ்! சரியாக சொன்னாய்!
இப்போது, பல வழிகளில் தோன்றும் பெருக்கல்களில் பகு எண்கள் இல்லாமல் பகாஎண்களை மட்டும் கருதிக்கொண்டால் கிடைப்பதைப் பாருங்கள் என ஆசிரியர் கூறினார்.
மாணவன் ஒருவன், 60-ஐ எப்படி எழுதினாலும் அதில் மொத்தத்தில் இரண்டு 2, ஒரு 3, ஒரு 5 ஆகிய பகா எண்கள் மட்டுமே வெவ்வேறு வரிசையில் அமைவதை காண முடிகிறது என்றான்.
சபாஷ்! சரியாக சொன்னாய். இந்த முடிவையே எண்ணியலின் அடிப்படைத் தேற்றம் விளக்குகிறது. இப்போது 1 என்ற எண்ணை
பகா எண்ணாக எடுத்துக்கொண்டு 6 என்ற எண்ணை பிரித்து எழுத முயல்வோம்.
6 = 1 × 2 × 3 = 1 × 1 × 2 × 3 = 1 × 1 × 1 × 2 × 3 = 1 × 1 × 1 × 1 × 2 × 3 = . . .
ஒன்றுடன் எந்த எண்ணை பெருக்கினாலும் அந்த எண்ணின் மதிப்பு மாறாமல் இருப்பதால், மேற்கண்ட பெருக்கல் வழிகளில் ஒரு 2, ஒரு 3 வருகிறது. ஆனால், 1 என்ற எண்ணை எத்தனை முறை வேண்டுமென்றாலும் எழுதமுடிவதைப் பார்க்கலாம்.
இதுவுமல்ல அதுவுமல்ல!
எனவே, 1 என்ற எண்ணை பகா எண்ணாக கருதினால், ஓர் இயல் எண்ணை ஒரே வழியில் பகா எண்களின் பெருக்கலாக எழுத முடியாது. இது எண்ணியலின் அடிப்படை தேற்றத்திற்கு முரணாக அமைவதை பாருங்கள். இதனாலேயே 1 ஐ பகா எண்களின் பட்டியிலில் சேர்க்கவில்லை.
அப்படியென்றால் அதை பகு எண்ணாக கருதலாமல்லவா? என ஓரு மாணவி கேட்டாள். 1 என்ற எண் அனைத்து இயல் எண்களையும் வகுக்கிறது, மேலும் அதற்கு 1 என ஒரே ஒரு வகுத்தி மட்டுமே உள்ளது. ஆனால், பகு எண்களுக்கு இரண்டிற்கு மேற்பட்ட வகுத்
திகள் இருக்க வேண்டுமல்லவா? இதனால் 1, பகு எண்களின் பட்டியலிலும் சேராது.
எனவே, 1 என்ற எண்ணை பகு எண்ணாகவும், பகா எண்ணாகவும் கருதமுடியாது என ஆசிரியர் தெளிவுபடுத்தினார்.
- கட்டுரையாளர், கணித ஆசிரியை, பை கணித மன்றம்.
FOLLOW US
Sign up to receive our newsletter in your inbox every day!
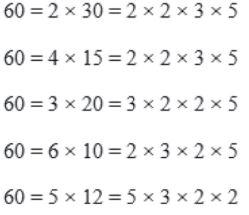


WRITE A COMMENT